|
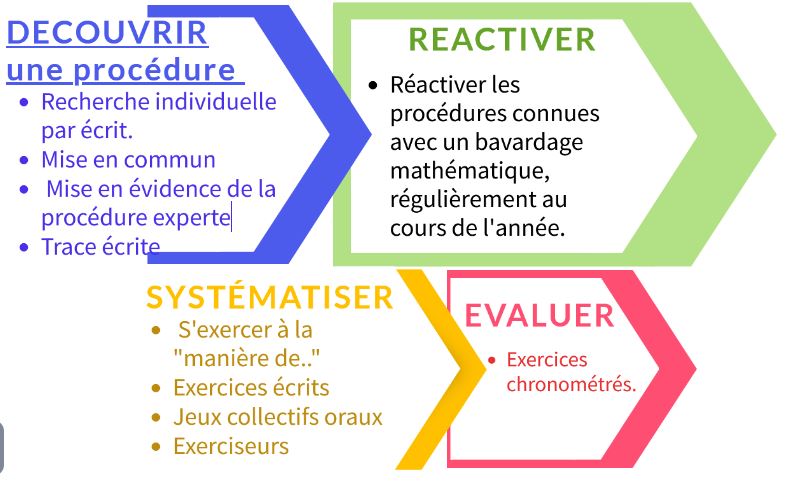
Les principes de cette procédure reprennent 5 situations distinguées par Brousseau pour l’enseignement des concepts mathématiques à l’école maternelle évoquées dans le guide sur la construction du nombre à l’école maternelle page 31 (la dévolution ; la situation d’action ; la situation de formulation ; la situation de validation ; l’institutionnalisation).
Objectifs :
|
| Compétences attendues
· En fonction du matériel à disposition, les élèves développeront des notions dans la construction du nombre, dans le domaine de la géométrie, et celui des mesures. · Reconnaître, nommer, décrire, comparer, ranger et classer des matières, des objets selon leurs qualités et leurs usages ; dénombrer, composer / décomposer, vocabulaire géométrique, se repérer dans le temps et l’espace. |
| En manipulant des objets variés, repérer des propriétés simples :
– Comparer : petit/grand, lourd/léger ; – Trier, classer, ranger (forme ; taille ; masse ; contenance…) ; – Représenter des quantités, décomposer, composer… ; – Situer des objets (les uns par rapport aux autres, par rapport à d’autres repères) ; – Reconnaître les différentes formes géométriques ; |
Démarche :
Le matériel est proposé dans des barquettes. En général, 3 matériels différents sont proposés par séance. Il doit y avoir autant de barquettes qui proposent le même matériel que d’élèves afin que chacun puisse choisir celui qu’il veut réellement. (et donc éviter la frustration.)
2. Donner une consigne : « trouver une bonne idée » ; Rôle de l’enseignant : L’enseignant découvre la bonne idée de l’élève en même temps que les autres élèves. Si besoin il accompagne individuellement chaque enfant lorsqu’il a terminé sa construction pour l’aider à verbaliser ce qu’il a fait
3. Lors d’un temps de présentation au groupe des constructions individuelles, Tout d’abord les autres élèves recherchent la bonne idée imaginée par l’élève, ils disent ce qu’ils voient, ce qu’ils reconnaissent en justifiant leur propos. L’enseignant « relance » avec des questions du type : Qu’est-ce qui te fait dire que… ? Explique-nous pourquoi… ? etc… C’est plutôt dans ce moment là que ressortent le plus souvent les nouvelles connaissances (et pas forcément lorsque l’élève présente sa bonne idée.) Le groupe négocie, observe, expérimente puis si pas de consensus, c’est l’enseignant qui tranche (vocabulaire, démonstration avec matériel…) Puis l’élève verbalise, explique aux autres ce qu’il a fait et en quoi c’est une bonne idée mathématique… A la fin du temps collectif, l’enseignant rappelle à l’oral ce que le groupe a appris ou a revu grâce aux bonnes idées des camarades. 4. Organiser une trace collectant ces « trouvailles ». Prévoir un espace d’affichage pour écrire les réalisations des élèves, et ajouter une photo (ou la production plane). Les élèves peuvent ainsi revenir sur les réalisations ; ces dernières peuvent être ensuite regrouper par domaine. On pourrait également imaginer un cahier de la classe des bonnes idées que les élèves pourraient aller consulter quand ils le souhaitent. Cliquer sur la première photo pour lancer le diaporama. 5. Une fois l’affiche réalisée, un travail de réinvestissement est proposé aux élèves sous la forme de petits ateliers qui reprennent les notions abordées pendant les «échanges mathématiques ». Pour aller plus loin : Les activités peuvent être présentées plusieurs fois de suite avec un même matériel. Les enfants auront la possibilité de « faire comme… » (reproduction d’une construction présentée par un autre élève) ou bien d’élaborer une autre idée. Demander de réaliser un dessin, de découpées des images (ou prédécoupées) dans papiers cadeaux ou bien trouvées dans des banques de données en rapport avec la vie de la classe |
Matériel utilisable :
Il est intéressant de mélanger le matériel, de l’associer à des contenants par exemple, des casiers, des constellations de dés … Cette réflexion autour de l’évolution enrichira les productions. |
| Rôle de l’enseignant :
Le travail de l’enseignant réside aussi en amont, dans la construction du matériel qui doit être attrayant, correspondre à l’univers des enfants et être évolutif quant aux notions maths qu’il peut induire. Une progression peut être construite. Être patient : quelle que soit la réalisation il y aura une verbalisation intéressante lors de la présentation au groupe. C’est grâce cette phase de présentation collective des « bonnes idées » que les réalisations deviendront de plus en plus élaborées. L’enseignant peut également trier les réalisations par domaines mathématiques. |
Merci à l’école de Saint Point pour les témoignages photos.